Many of us fall in the trap of blithely distinguishing recursion and iteration syntactically: recursion is a function that calls itself over and over again, and iteration is a for, while or whatever looping construct available in new trendy languages. This distinction is not incorrect; it is merely imprecise. We must differentiate between syntax and process.

Recursive and iterative processes

Before you ask, no, I’m not refering to the processes you’ll find in your operating system but to a systematic series of actions directed to some end.

A recursive process evolves as a chain of deferred operations. Take, for example, the factorial procedure represented as a recursive process ¹:

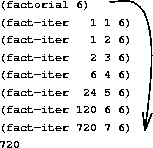
In contrast, an iterative process can be described as a set of state variables that change as the process evolves. It does not grow and shrink like a recursive process ² .

The key difference between the two is where the state of the process is maintained. For a recursive process, the state is “hidden” in the call stack while for an iterative process, the state is kept in a set of variables. To put it crudely, the difference can be reduced to the choice of data structure to track the evolution of the process.

Structure and Interpretation of Computer Programs provides a thorough explanation of iterative and recursive processes.

Syntax vs Process

It is important to understand that a process is independent of the syntax it is written in: iterative syntax can describe both an iterative and a recursive process, and the same goes for recursive syntax.

Let’s examine each case one by one.

Recursive syntax to recursive process

This case is the first of two which most of us are familiar with. It corresponds to a recursive function which is not tail recursive³ ; tail recursive functions don’t defer operations, and therefore don’t fit into this category.

For example, the following snippet fits into case.

function factorial(n) {
    if (n == 0) {
	return 1;
    }
    
    return n * factorial(n - 1);
}

Note that since the return value is not solely factorial(n - 1) but an expression which contains factorial(n - 1), this function is not tail recursive.

Iterative syntax to recursive process

This case is more theoretical than practical. Describing a recursive process with iterative syntax means you’ll have to

1. build the algorithm around a looping construct
2. manage a stack stored in a state variable as a means to defer operations.

Let’s see how we would write the factorial function.

function factorial(n) {
    if (n == 0) {
	return 1;
    }
    
    var stack = [];
    var result = 1;

    stack.push(n--);
    while (stack.length > 0) {
	if (n > 0) {
	    stack.push(n--);
	}
	else {
	    result *= stack.pop();
	}
    }
    return result;
}

This is impractical at best. Note that this has the same computational effect as the previous case which was written using recursive syntax. This leads to an interesting observation: when describing a recursive process, recursive syntax hides computation! In other words, recursive syntax is declarative knowledge while iterative syntax is procedural knowledge ⁴ .

Iterative syntax to iterative process

This is the second case of two which most of us are familiar with. 99% ⁵ of the code written using a looping construct (for, while, do...while, etc) corresponds to this case. Let’s see how we would write the factorial function using this technique.

function factorial(n) {
    var result = 1;
    while (n > 0) {
	result *= n;
	n--;
    }
    
    return result;
}

The defining characteristic is that no state variable (i.e. stack) is used as a means to defer operations. Since this is the case introduced to the majority of new programmers, we’ll consider it trivial and won’t discuss it in greater detail.

Recursive syntax to iterative process

This last case is only possible in languages that support tail call optimization (TCO). The defining characteristic of a recursive procedure that describes an iterative process is that the state of the computation is captured completely in the procedure’s arguments; the call stack plays no role in the computation. It follows inexorably that the procedure must be tail recursive.

Take the following example: a factorial function written in JavaScript. Note that JavaScript does not support tail call optimization; we choose this language because most programmers are familiar with the syntax.

function factorial(n) {
    return fact_iter(1, 1, n);
}

// Recursive syntax, iterative process
function fact_iter(product, counter, max) {
  if (counter > max) {
     return product;
  }
  return fact_iter(product * counter, counter + 1, max);
}

When written in a language equipped with tail call optimization, fact_iter has the same computational effect as when written using a looping construct.

Implementation Details

In order to use recursion and iteration appropriately, it is important to understand the difference between how recursive steps and iteration steps interact. By interact, we mean the different ways in which an iterative or recursive step influences the previous or following one.

Iteration

Absent of a call stack, each iteration step can only interact with the subsequent one because there is no concept of deferred operation. That interaction can only be done by assigning to or mutating a state variable. Note that a state variable is a variable outside the block when using iterative syntax and is an argument (or a free variable) when using recursive syntax.

As we can see, iteration steps are pretty limited in how they can influence the next. With recursion, it is a different story.

Recursion

Recursive steps have a total of three different ways to interact, two involving mutation. The reason is that recursion has deferred operations. This means that each recursive step can not only communicate to the subsequent one but also to the previous one! “Why should I care?”, you say? We’re getting there.

Interacting with the subsequent recursive step is boring; it is no different than with iteration. What is of interest to us is how we communicate back to the previous step.

We wrote the examples in the diagram using recursive syntax because it’s much cleaner than iterative syntax and most if not all programmers are used to see it written this way.

1. Using the return value

Perhaps the most obvious and ubiquitous way to communicate back to the caller is by returning a value. This strategy abides by the functional programming paradigm. When used in a recursive context, say when building a recursive structure such as a tree, we expect the “deepest” stack frame to build the initial structure and return it to its caller. Subsequent frames build upon this structure and return it further up the chain, all the way to the first frame, where we ultimately end up with the final “version” of the recursive structure.

2. Assigning to or mutating a free variable

Enter the realm of mutation. A free variable is any variable that is not in the current scope but is still accessible. In C, for example, this corresponds to the notorious global variables.

Joke break:
Q: What’s the best naming prefix for a global variable?
A: //

Every stack frame of a recursive function sees the same free variables, and therefore any assignment or mutation will be seen by all stack frames. This is generally considered bad style, as depicted during the joke break.

3. Mutating an argument

The last option for stack frames to interact is by mutating an argument. Note that, in contrast with free variables, assigning to an argument is not an option. See pointer aliasing. Mutating an argument can be seen as the middle ground between returning a value and modifying a free variable. It’s not as functionally pure as returning a value, but not as bad a mutating a free variable: it’s mutating a variable that was given to you by your caller. However, this distinction is more pragmatic than real. You very well could pass in a free variable to a function as an argument, and have that function modify the argument, essentially leading to the same result as if the function had modified the free variable directly. We’ll prefer to ignore pedantries such as this one.

Now why did we go in all this trouble? Sure, when dealing with trivial problems, taking the time to understand the different options you have to design your recursive algorithm is most likely useless. However, having a clear picture of these cases in your head is very important when approaching harder problems. Let’s see how we would approach such a one.

Use case: parsing a stream of tokens

Parsing a stream of tokens happens literally all the time in compilers. When parsing source code, a token corresponds to a “word”: int, function, my_variable, {, }, (, ), etc. The stream is a list made up of all the tokens in the order they were read in. For example,

int x = 3;

would yield the following stream of tokens:

int -> x -> = -> 3 -> ;

We’re especially interested in streams of tokens with a recursive structure: source code is a classic example, but we’re also thinking JSON strings, XML, etc. Why so? Because the parsing phase will output a tree (asbtract syntax tree in the case of source code). And how are we going to build that tree? You guessed it: recursively, using the techniques described in the previous section!

Unlike most recursive problems where every recursive step must return one piece of information to its caller (e.g. factorial of n - 1 in the case of the recursive factorial procedure), this problem requires of every recursive step to communicate two pieces of information: an updated stream of tokens (the original minus the consumed tokens) and the subtree resulting from the consumed tokens. As the designer of the recursive algorithm, you can choose one of the three strategies for communicating back the two different pieces of information.

The following diagram illustrates this:

The keen eye for detail will have noticed that we didn’t include the “assign to or mutate free variable” case; we deliberately did so because it is very bug prone and shouldn’t be used in practice.

This use case sums it all up! We chose recursion over iteration because deferred operations are natural when dealing with recursive structures. We then noticed that two pieces of information needed to be communicated between recursive steps: the updated stream of tokens and a subtree. Knowing we have two communication options per piece of information (not considering “assign to or mutate free variable” which encourages bad style), we knew right away that there would be four possible general frameworks for our algorithm (2 pieces of information x 2 communication options).

Now that we clearly see the big picture, we are poised to choose the best algorithm framework based on our constraints, preferences, etc.

• ← Previous Post
• Next Post →